Transformações Linares em 2D

Uma planilha que demonstra a matemática de matrizes usada para redimensionar, rotacionar e esticar cada caractere das fontes do seu editor de textos.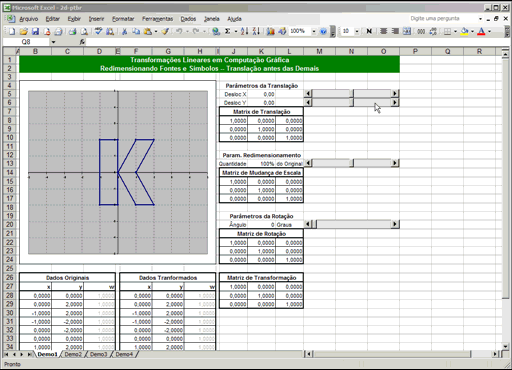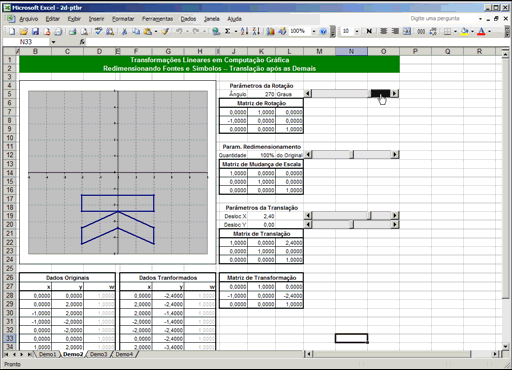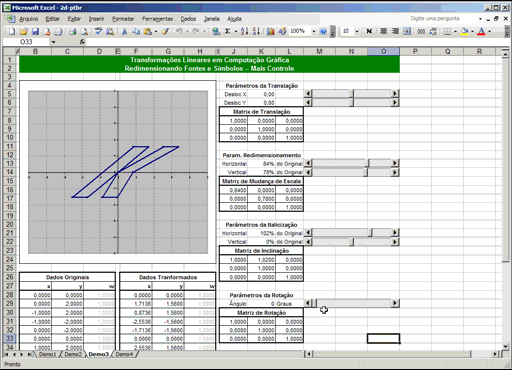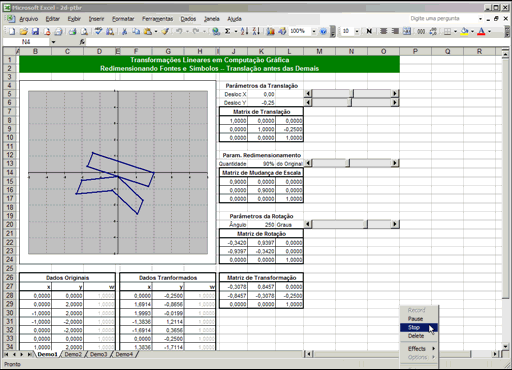

Clique na figura para baixar a planilha

• Notas: Fica melhor em 1024x768. Pode ser necessário alterá-la para ficar bom em resoluções menores.

Transformações Lineares

Cada planilha tem barras de rolagem que lhe permitem mover, girar e redimensionar o desenho no gráfico. Experimente brincar com elas.

O primeiro passo de qualquer coisa em computação gráfica é obter um modelo matemático do objeto. Você verá isso nas tabelas "Dados Originais" logo abaixo dos gráficos. Nas primeiras três planilhas, usamos um modelo de 12 pontos de uma letra "K" estilizada. As coordenadas de cada ponto são números inteiros, facilitando correlacionar cada ponto na tabela com seus respectivos pontos no gráfico -- tente mudar algum número o gráfico instantaneamente mudará, tornando visualmente óbvio o ponto que você alterou. Não se dê ao trabaho de mexer nos "w" (os que são todos 1) -- veremos mais abaixo para que eles servem.

Na última planilha, usamos um modelo de 60 pontos de uma letra "C" ornamental, mostrada em duas versões: na primeira pode-se notar que, quando a amplação é grande, ela não fica muito bonita devido ao fato dos pontos serem unidos por linhas retas. O segundo gráfico é o mesmo do primeiro, mas com o recurso de "suavização" do Excel ligado. Eu certamente poderia ter caprichado um pouco mais no modelo para torná-lo ainda mais bonito, mas acho que me falta o talento artístico para isso.

As barras de rolagem controlam parâmetros das matrizes de transformação para cada operação primitiva. Então calculamos a transformação composta -- nada mais que a multiplicação das matrizes. Então multiplicamos essa matriz combinada por cada ponto da tabela "Dados Originais", resultando no modelo transformado, que finalmente é usado para desenhar o gráfico (descartando-se o "1" final de cada ponto).

Se você é um estudante secundarista que teve álgebra matricial empurrada goela abaixo sem nunca saber para que ela servia... bem, agora você sabe. Essa é a matemática que lhe permite obter caracteres de diferentes tamanhos quando você clica na caixa "tamanho da fonte" no seu editor de texto ou que lhe permite rotacionar as letras e formas no Corel Draw.

E sim, é uma calculeira danada que pouca gente teria paciência de fazer à mão. É para isso que servem os computadores: para fazer as contas que nós, humanos, somos lerdos demais pra fazer. E pra isso servem os programadores de computadores: para transformar a matemática em coisas úteis.

A única diferença entre a primeira e a segunda planilhas é a ordem em que as matrizes foram multiplicadas. Isso ilustra visualmente o fato da multiplicação de matrizes ser não-comutativa (ou seja, a ordem dos fatores altera, sim, o produto): na primeira planilha, o modelo roda ao redor do seu "centro", independente de para onde você o mova, porque a rotação foi feita antes da translação; na segunda planilha, ele sempre roda ao redor da origem, porque a rotação foi feita após a translação.

Rotações, mudanças de escala e cisalhamentos podem ser facilmente representados por matrizes, mas translações normalmente não. Para resolver isso, empregamos um truque legal inventado por Möbius no século 18 chamado coordenadas homogêneas: para os pontos, usamos vetores de 3 colunas ao invés de duas, preenchendo a última coluna com o número 1. Adicionalmente, usamos uma matriz 3x3 ao invés de 2x2: a última coluna contém o deslocamento X, Y e o número 1. Assim, quando multiplicarmos as matrizes, os "1" finais nos vetores farão os deslocamentos das translação passarem direto, sem alterações, de forma a serem adicionados às coordenadas em questão. A última linha (0,0,1) na matriz perpetua os "uns" nos vetores resultantes.

Esse conjunto de planilhas usa um recurso obscuro mas muito útil do Excel: as fórmulas podem retornar mais de um único resultado -- todas as funções de matrizes fazem isso. Quando esse for o caso, você deve selecionar toda a faixa de células que receberá o resultado e terminar de editar a fórmula com ALT+ENTER, ao invés de apenas ENTER.

Eu poderia perfeitamente ter feito a aritmética de matrizes usando somas e multiplicações normais, sem usar as funções de manipulação de matrizes embutidas no Excel, mas achei que da forma que eu fiz ficaria mais fácil de entender.

Eu também poderia perfeitamente otimizado um pouco os cálculos, removendo as últimas linhas desnecessárias e não incluíndo as colunas "1" finais em cada ponto (e suas respectivas multiplicações redundantes), mas, novamente, deixei assim mesmo para maior clareza.

Mini-FAQ

P1. Como você faz para as barras de rolagem mudarem os valores das células? Há algum código VBA escondido?

R1. Não. Com efeito, eu acho que a beleza da coisa é que não há código VBA em absoluto.

De fato, barras de rolagem e outros controles de formulário poderem mudar os valores de algumas células é um recurso padrão (ainda que surpreendentemente desconhecido) do Excel há mais de uma década.

Eis como usá-lo: clique com o botão direito em qualquer ícone da barra de ferramentas -- um menu pop-up lhe permitirá escolher outras barras de ferramentas. Clique na opção "Formulário"; isso fará com que a barra de ferramentas de controles de formulário (normalmente desativada) passe a aparecer. Nela você pode selecionar vários controles, inclusive as barras de rolagem: clique no ícone do controle desejado e o cursor do mouse mudará para uma cruz fina. Daí, arraste-e-solte um retângulo na planilha e um controle daquele tamanho aparecerá. Clique no botão direito sobre o controle recém criado para chamar seu menu de contexto e peça a opçao "Formatar controle". Uma caixa de diálogo aparece onde você pode definir os valores máximos e mínimos do controle, os incrementes, e, mais importante, a que célula ele está associado.

Tão logo você associe um controle a uma célula, toda vez que você clicar naquele controle, fazendo com que mude de valor, ele vai disparar um recálculo (assumindo que o recálculo automático esteja globalmente habilitado, o que provavelmente está, pois é o padrão.) Se algum gráfico depender de alguma célula que em última instância dependa de alguma célula vinculada àquele controle, ele será redesenhado também.

Nas versões do Excel 2003 e superiores, é útil circundar o gráfico com células cujos valores mudam durante o recálculo, para forçar o gráfico a ficar contido no retângulo de atualização. Doutra feita, o gráfico poderá ser apenas particialmente redesenhado (ou não ser redesenhado em absoluto), fazendo as animações ficarem feiosas.

Incidentalmente, o OpenOffice tem um recurso similar que funciona quase exatamente da mesma forma, mas o redesenho leva vários segundos, tornando lerdo demais para animações. Além disso, os recursos de gráfico do OO ficam muito atrás dos do Excel -- até hoje eu não entendo por que os gráficos XY do OO ainda não suportam algo tão simples quanto valores de X fora de ordem. É por isso que eu não disponibilizo versões dessa planilha para o OO.
topo